MAST3
Multidisciplinary-design Adaptation and Sensitivity Toolkit (MAST)
Functions
MAST::Optimization::Aggregation Namespace Reference

Functions

template<typename ScalarType >
ScalarType aggregate_maximum (const libMesh::Parallel::Communicator *comm, const std::vector< ScalarType > &vec, const real_t p)
 computes aggregated maximum of values specified in vector vec. More...
 
template<typename ScalarType >
void aggregate_maximum_denominator (const libMesh::Parallel::Communicator *comm, const std::vector< ScalarType > &vec, const real_t p, ScalarType &denom, ScalarType &v_max)
 Computes the denominator of the sensitivity of aggregated maximum function for use in later sensitivity computations. More...
 
template<typename ScalarType >
ScalarType aggregate_maximum_sensitivity (const libMesh::Parallel::Communicator *comm, const std::vector< ScalarType > &vec, const uint_t i, const real_t p)
 computes sensitivity of aggregated maximum of values specified in vector vec with respect to i th value. More...
 
template<typename ScalarType >
ScalarType aggregate_maximum_sensitivity (const libMesh::Parallel::Communicator *comm, const std::vector< ScalarType > &vec, const std::vector< ScalarType > &dvec, const real_t p)
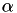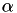 computes sensitivity of aggregated maximum of values specified in vector vec with respect to parameter $ \alpha $. More...
 
template<typename ScalarType >
ScalarType aggregate_maximum_sensitivity (const std::vector< ScalarType > &vec, const uint_t i, const real_t p, const ScalarType &denom, const ScalarType &v_max)
 computes sensitivity of aggregated maximum of values specified in vector vec with respect to i th value. More...
 
template<typename ScalarType >
ScalarType aggregate_maximum_sensitivity (const libMesh::Parallel::Communicator *comm, const std::vector< ScalarType > &vec, const std::vector< ScalarType > &dvec, const real_t p, const ScalarType &denom, const ScalarType &v_max)
 computes sensitivity of aggregated maximum of values specified in vector vec with respect to parameter $ \alpha $. More...
 
template<typename ScalarType >
ScalarType aggregate_minimum (const libMesh::Parallel::Communicator *comm, const std::vector< ScalarType > &vec, const real_t p)
 computes aggregated minimum of values specified in vector vec. More...
 
template<typename ScalarType >
void aggregate_minimum_denominator (const libMesh::Parallel::Communicator *comm, const std::vector< ScalarType > &vec, const real_t p, ScalarType &denom, ScalarType &v_min)
 Computes the denominator of the sensitivity of aggregated minimum function for use in later sensitivity computations. More...
 
template<typename ScalarType >
ScalarType aggregate_minimum_sensitivity (const libMesh::Parallel::Communicator *comm, const std::vector< ScalarType > &vec, const uint_t i, const real_t p)
 computes sensitivity of aggregated minimum of values specified in vector vec with respect to i th value. More...
 
template<typename ScalarType >
ScalarType aggregate_minimum_sensitivity (const libMesh::Parallel::Communicator *comm, const std::vector< ScalarType > &vec, const std::vector< ScalarType > &dvec, const real_t p)
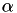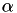 computes sensitivity of aggregated minimum of values specified in vector vec with respect to parameter $ \alpha $. More...
 
template<typename ScalarType >
ScalarType aggregate_minimum_sensitivity (const std::vector< ScalarType > &vec, const uint_t i, const real_t p, const ScalarType &denom, const ScalarType &v_min)
 computes sensitivity of aggregated minimum of values specified in vector vec with respect to i th value. More...
 
template<typename ScalarType >
ScalarType aggregate_minimum_sensitivity (const libMesh::Parallel::Communicator *comm, const std::vector< ScalarType > &vec, const std::vector< ScalarType > &dvec, const real_t p, const ScalarType &denom, const ScalarType &v_min)
 computes sensitivity of aggregated minimum of values specified in vector vec with respect to parameter $ \alpha $. More...
 

Function Documentation

◆ aggregate_maximum()

template<typename ScalarType >
ScalarType MAST::Optimization::Aggregation::aggregate_maximum ( const libMesh::Parallel::Communicator *  comm,
const std::vector< ScalarType > &  vec,
const real_t  p 
)

computes aggregated maximum of values specified in vector vec.

The aggregation constant is p. The aggregation expression used is

\[ v_{agg} = v_{max} + \frac{1}{p} \log \left( \sum_i \exp (p (v_i - v_{max})) \right) \]

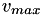, where, $ v_{max} $ is the maximum value out of all values in vec. If comm is a non-null pointer then the computation is synchronized across all ranks with the 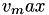$ v_max$ and the summation obtained from a collective.

Definition at line 248 of file discrete_aggregation.hpp.

250  {
251 
252  ScalarType
253  v = 0.,
254  v_max = 0.;
255 
256  v_max = MAST::Numerics::Utility::real_maximum(vec);
257 
258  if (comm) MAST::Numerics::Utility::comm_max(*comm, v_max);
259 
260  for (uint_t i=0; i<vec.size(); i++) {
261 
262  v += exp(p * (vec[i] - v_max));
263  }
264 
265  if (comm) MAST::Numerics::Utility::comm_sum(*comm, v);
266 
267  v = v_max + log(v) / p;
268 
269  return v;
270 }
MAST::Numerics::Utility::comm_max
real_t comm_max(const libMesh::Parallel::Communicator &comm, const std::vector< real_t > &v)
Definition: utility.hpp:422
MAST::Numerics::Utility::real_maximum
real_t real_maximum(const std::vector< real_t > &vec)
computes maximum of vector
Definition: utility.hpp:141
uint_t
unsigned int uint_t
Definition: mast_data_types.h:43
MAST::Numerics::Utility::comm_sum
void comm_sum(const libMesh::Parallel::Communicator &comm, real_t &v)
Definition: utility.hpp:328

◆ aggregate_maximum_denominator()

template<typename ScalarType >
void MAST::Optimization::Aggregation::aggregate_maximum_denominator ( const libMesh::Parallel::Communicator *  comm,
const std::vector< ScalarType > &  vec,
const real_t  p,
ScalarType &  denom,
ScalarType &  v_max 
)

Computes the denominator of the sensitivity of aggregated maximum function for use in later sensitivity computations.

The value is 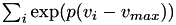$ \sum_i \exp (p (v_i - v_{max})) $, where, 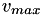$ v_{max} $ is the maximum value out of all values in vec. The denominator is returned in denom and the minimum value is returned in v_max. If comm is a non-null pointer then the computation is synchronized across all ranks with the 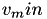$ v_min$ and the summation obtained from a collective.

Definition at line 362 of file discrete_aggregation.hpp.

366  {
367 
368  denom = 0.;
369 
370  v_max = MAST::Numerics::Utility::real_maximum(vec);
371 
372  if (comm) MAST::Numerics::Utility::comm_max(*comm, v_max);
373 
374  for (uint_t i=0; i<vec.size(); i++) {
375 
376  denom += exp(p * (vec[i] - v_max));
377  }
378 
379  if (comm) MAST::Numerics::Utility::comm_sum(*comm, denom);
380 }
MAST::Numerics::Utility::comm_max
real_t comm_max(const libMesh::Parallel::Communicator &comm, const std::vector< real_t > &v)
Definition: utility.hpp:422
MAST::Numerics::Utility::real_maximum
real_t real_maximum(const std::vector< real_t > &vec)
computes maximum of vector
Definition: utility.hpp:141
uint_t
unsigned int uint_t
Definition: mast_data_types.h:43
MAST::Numerics::Utility::comm_sum
void comm_sum(const libMesh::Parallel::Communicator &comm, real_t &v)
Definition: utility.hpp:328

◆ aggregate_maximum_sensitivity() [1/4]

template<typename ScalarType >
ScalarType MAST::Optimization::Aggregation::aggregate_maximum_sensitivity ( const libMesh::Parallel::Communicator *  comm,
const std::vector< ScalarType > &  vec,
const uint_t  i,
const real_t  p 
)

computes sensitivity of aggregated maximum of values specified in vector vec with respect to i th value.

The aggregation constant is p. The aggregation expression used is

\[ \frac{d v_{agg}}{d v_j} = \frac{ \exp ( p (v_j - v_{max})) }{ \sum_i \exp ( p (v_i - v_{max})) } \]

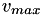, where, $ v_{max} $ is the maximum value out of all values in vec. If comm is a non-null pointer then the computation is synchronized across all ranks with the 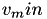$ v_min$ and the summation obtained from a collective.

Definition at line 284 of file discrete_aggregation.hpp.

287  {
288 
289  ScalarType
290  v = 0.,
291  v_max = 0.;
292 
293  v_max = MAST::Numerics::Utility::real_maximum(vec);
294 
295  if (comm) MAST::Numerics::Utility::comm_max(*comm, v_max);
296 
297  for (uint_t i=0; i<vec.size(); i++) {
298 
299  v += exp(p * (vec[i] - v_max));
300  }
301 
302  if (comm) MAST::Numerics::Utility::comm_sum(*comm, v);
303 
304  v = exp(p * (vec[i] - v_max)) / v;
305 
306  return v;
307 }
MAST::Numerics::Utility::comm_max
real_t comm_max(const libMesh::Parallel::Communicator &comm, const std::vector< real_t > &v)
Definition: utility.hpp:422
MAST::Numerics::Utility::real_maximum
real_t real_maximum(const std::vector< real_t > &vec)
computes maximum of vector
Definition: utility.hpp:141
uint_t
unsigned int uint_t
Definition: mast_data_types.h:43
MAST::Numerics::Utility::comm_sum
void comm_sum(const libMesh::Parallel::Communicator &comm, real_t &v)
Definition: utility.hpp:328

◆ aggregate_maximum_sensitivity() [2/4]

template<typename ScalarType >
ScalarType MAST::Optimization::Aggregation::aggregate_maximum_sensitivity ( const libMesh::Parallel::Communicator *  comm,
const std::vector< ScalarType > &  vec,
const std::vector< ScalarType > &  dvec,
const real_t  p 
)

computes sensitivity of aggregated maximum of values specified in vector vec with respect to parameter 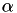$ \alpha $.

The aggregation constant is p. The sensitivity of values with respect to parameter is provided in dvec. The sensitivity expression used is

\[ \frac{d v_{agg}}{d p} = \frac{ \sum_j \exp ( p (v_j - v_{max})) \frac{dv_j}{d\alpha} }{ \sum_i \exp ( p (v_i - v_{max})) } \]

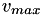, where, $ v_{max} $ is the maximum value out of all values in vec. If comm is a non-null pointer then the computation is synchronized across all ranks with the 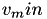$ v_min$ and the summation obtained from a collective.

Definition at line 323 of file discrete_aggregation.hpp.

326  {
327 
328  ScalarType
329  dv = 0.,
330  v = 0.,
331  v_max = 0.;
332 
333  v_max = MAST::Numerics::Utility::real_maximum(vec);
334 
335  if (comm) MAST::Numerics::Utility::comm_max(*comm, v_max);
336 
337  for (uint_t i=0; i<vec.size(); i++) {
338 
339  dv += exp(p * (vec[i] - v_max)) * dvec[i];
340  v += exp(p * (vec[i] - v_max));
341  }
342 
343  if (comm) MAST::Numerics::Utility::comm_sum(*comm, dv);
344  if (comm) MAST::Numerics::Utility::comm_sum(*comm, v);
345 
346  v = dv / v;
347 
348  return v;
349 }
MAST::Numerics::Utility::comm_max
real_t comm_max(const libMesh::Parallel::Communicator &comm, const std::vector< real_t > &v)
Definition: utility.hpp:422
MAST::Numerics::Utility::real_maximum
real_t real_maximum(const std::vector< real_t > &vec)
computes maximum of vector
Definition: utility.hpp:141
uint_t
unsigned int uint_t
Definition: mast_data_types.h:43
MAST::Numerics::Utility::comm_sum
void comm_sum(const libMesh::Parallel::Communicator &comm, real_t &v)
Definition: utility.hpp:328

◆ aggregate_maximum_sensitivity() [3/4]

template<typename ScalarType >
ScalarType MAST::Optimization::Aggregation::aggregate_maximum_sensitivity ( const std::vector< ScalarType > &  vec,
const uint_t  i,
const real_t  p,
const ScalarType &  denom,
const ScalarType &  v_max 
)

computes sensitivity of aggregated maximum of values specified in vector vec with respect to i th value.

The aggregation constant is p. The aggregation expression used is

\[ \frac{d v_{agg}}{d v_j} = \frac{ \exp (p (v_j - v_{max})) }{ \sum_i \exp (p (v_i - v_{max})) } \]

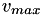, where, $ v_{max} $ is the maximum value out of all values in vec. This method differs from the other in that the user provides the cached denominator of the sensitivity and the maximum value in denom and v_max.

Definition at line 395 of file discrete_aggregation.hpp.

399  {
400 
401  return exp(p * (vec[i] - v_max)) / denom;
402 }

◆ aggregate_maximum_sensitivity() [4/4]

template<typename ScalarType >
ScalarType MAST::Optimization::Aggregation::aggregate_maximum_sensitivity ( const libMesh::Parallel::Communicator *  comm,
const std::vector< ScalarType > &  vec,
const std::vector< ScalarType > &  dvec,
const real_t  p,
const ScalarType &  denom,
const ScalarType &  v_max 
)

computes sensitivity of aggregated maximum of values specified in vector vec with respect to parameter 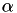$ \alpha $.

The aggregation constant is p. The sensitivity of values with respect to parameter is provided in dvec. The sensitivity expression used is

\[ \frac{d v_{agg}}{d p} = \frac{ \sum_j \exp (p (v_j - v_{max})) \frac{dv_j}{d\alpha} }{ \sum_i \exp (p (v_i - v_{max})) } \]

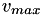, where, $ v_{max} $ is the maximum value out of all values in vec. This method differs from the other in that the user provides the cached denominator of the sensitivity and the maximum value in denom and v_max. If comm is a non-null pointer then the computation is synchronized across all ranks with the 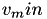$ v_min$ and the summation obtained from a collective.

Definition at line 420 of file discrete_aggregation.hpp.

425  {
426 
427  ScalarType
428  dv = 0.;
429 
430  for (uint_t i=0; i<vec.size(); i++) {
431 
432  dv += exp(p * (vec[i] - v_max)) * dvec[i];
433  }
434 
435  if (comm) MAST::Numerics::Utility::comm_sum(*comm, dv);
436 
437  return dv / denom;
438 }
uint_t
unsigned int uint_t
Definition: mast_data_types.h:43
MAST::Numerics::Utility::comm_sum
void comm_sum(const libMesh::Parallel::Communicator &comm, real_t &v)
Definition: utility.hpp:328

◆ aggregate_minimum()

template<typename ScalarType >
ScalarType MAST::Optimization::Aggregation::aggregate_minimum ( const libMesh::Parallel::Communicator *  comm,
const std::vector< ScalarType > &  vec,
const real_t  p 
)

computes aggregated minimum of values specified in vector vec.

The aggregation constant is p. The aggregation expression used is

\[ v_{agg} = v_{min} - \frac{1}{p} \log \left( \sum_i \exp (-p (v_i - v_{min})) \right) \]

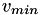, where, $ v_{min} $ is the minimum value out of all values in vec. If comm is a non-null pointer then the computation is synchronized across all ranks with the 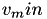$ v_min$ and the summation obtained from a collective.

Definition at line 44 of file discrete_aggregation.hpp.

46  {
47 
48  ScalarType
49  v = 0.,
50  v_min = 0.;
51 
52  v_min = MAST::Numerics::Utility::real_minimum(vec);
53 
54  if (comm) MAST::Numerics::Utility::comm_min(*comm, v_min);
55 
56  for (uint_t i=0; i<vec.size(); i++) {
57 
58  v += exp(-p * (vec[i] - v_min));
59  }
60 
61  if (comm) MAST::Numerics::Utility::comm_sum(*comm, v);
62 
63  v = v_min - log(v) / p;
64 
65  return v;
66 }
MAST::Numerics::Utility::real_minimum
real_t real_minimum(const std::vector< real_t > &vec)
computes minimum of vector
Definition: utility.hpp:92
MAST::Numerics::Utility::comm_min
real_t comm_min(const libMesh::Parallel::Communicator &comm, const std::vector< real_t > &v)
Definition: utility.hpp:382
uint_t
unsigned int uint_t
Definition: mast_data_types.h:43
MAST::Numerics::Utility::comm_sum
void comm_sum(const libMesh::Parallel::Communicator &comm, real_t &v)
Definition: utility.hpp:328

◆ aggregate_minimum_denominator()

template<typename ScalarType >
void MAST::Optimization::Aggregation::aggregate_minimum_denominator ( const libMesh::Parallel::Communicator *  comm,
const std::vector< ScalarType > &  vec,
const real_t  p,
ScalarType &  denom,
ScalarType &  v_min 
)

Computes the denominator of the sensitivity of aggregated minimum function for use in later sensitivity computations.

The value is 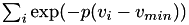$ \sum_i \exp (-p (v_i - v_{min})) $, where, 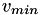$ v_{min} $ is the minimum value out of all values in vec. The denomimator is returned in denom and the minimum value is returned in vmin. If comm is a non-null pointer then the computation is synchronized across all ranks with the 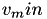$ v_min$ and the summation obtained from a collective.

Definition at line 159 of file discrete_aggregation.hpp.

163  {
164 
165  denom = 0.;
166 
167  v_min = MAST::Numerics::Utility::real_minimum(vec);
168 
169  if (comm) MAST::Numerics::Utility::comm_min(*comm, v_min);
170 
171  for (uint_t i=0; i<vec.size(); i++) {
172 
173  denom += exp(-p * (vec[i] - v_min));
174  }
175 
176  if (comm) MAST::Numerics::Utility::comm_sum(*comm, denom);
177 }
MAST::Numerics::Utility::real_minimum
real_t real_minimum(const std::vector< real_t > &vec)
computes minimum of vector
Definition: utility.hpp:92
MAST::Numerics::Utility::comm_min
real_t comm_min(const libMesh::Parallel::Communicator &comm, const std::vector< real_t > &v)
Definition: utility.hpp:382
uint_t
unsigned int uint_t
Definition: mast_data_types.h:43
MAST::Numerics::Utility::comm_sum
void comm_sum(const libMesh::Parallel::Communicator &comm, real_t &v)
Definition: utility.hpp:328

◆ aggregate_minimum_sensitivity() [1/4]

template<typename ScalarType >
ScalarType MAST::Optimization::Aggregation::aggregate_minimum_sensitivity ( const libMesh::Parallel::Communicator *  comm,
const std::vector< ScalarType > &  vec,
const uint_t  i,
const real_t  p 
)

computes sensitivity of aggregated minimum of values specified in vector vec with respect to i th value.

The aggregation constant is p. The aggregation expression used is

\[ \frac{d v_{agg}}{d v_j} = \frac{ \exp (-p (v_j - v_{min})) }{ \sum_i \exp (-p (v_i - v_{min})) } \]

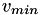, where, $ v_{min} $ is the minimum value out of all values in vec. If comm is a non-null pointer then the computation is synchronized across all ranks with the 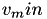$ v_min$ and the summation obtained from a collective.

Definition at line 80 of file discrete_aggregation.hpp.

83  {
84 
85  ScalarType
86  v = 0.,
87  v_min = 0.;
88 
89  v_min = MAST::Numerics::Utility::real_minimum(vec);
90 
91  if (comm) MAST::Numerics::Utility::comm_min(*comm, v_min);
92 
93  for (uint_t i=0; i<vec.size(); i++) {
94 
95  v += exp(-p * (vec[i] - v_min));
96  }
97 
98  if (comm) MAST::Numerics::Utility::comm_sum(*comm, v);
99 
100  v = exp(-p * (vec[i] - v_min)) / v;
101 
102  return v;
103 }
MAST::Numerics::Utility::real_minimum
real_t real_minimum(const std::vector< real_t > &vec)
computes minimum of vector
Definition: utility.hpp:92
MAST::Numerics::Utility::comm_min
real_t comm_min(const libMesh::Parallel::Communicator &comm, const std::vector< real_t > &v)
Definition: utility.hpp:382
uint_t
unsigned int uint_t
Definition: mast_data_types.h:43
MAST::Numerics::Utility::comm_sum
void comm_sum(const libMesh::Parallel::Communicator &comm, real_t &v)
Definition: utility.hpp:328

◆ aggregate_minimum_sensitivity() [2/4]

template<typename ScalarType >
ScalarType MAST::Optimization::Aggregation::aggregate_minimum_sensitivity ( const libMesh::Parallel::Communicator *  comm,
const std::vector< ScalarType > &  vec,
const std::vector< ScalarType > &  dvec,
const real_t  p 
)

computes sensitivity of aggregated minimum of values specified in vector vec with respect to parameter 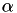$ \alpha $.

The aggregation constant is p. The sensitivity of values with respect to parameter is provided in dvec. The sensitivity expression used is

\[ \frac{d v_{agg}}{d p} = \frac{ \sum_j \exp (-p (v_j - v_{min})) \frac{dv_j}{d\alpha} }{ \sum_i \exp (-p (v_i - v_{min})) } \]

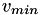, where, $ v_{min} $ is the minimum value out of all values in vec. If comm is a non-null pointer then the computation is synchronized across all ranks with the 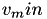$ v_min$ and the summation obtained from a collective.

Definition at line 119 of file discrete_aggregation.hpp.

122  {
123 
124  ScalarType
125  dv = 0.,
126  v = 0.,
127  v_min = 0.;
128 
129  v_min = MAST::Numerics::Utility::real_minimum(vec);
130 
131  if (comm) MAST::Numerics::Utility::comm_min(*comm, v_min);
132 
133  for (uint_t i=0; i<vec.size(); i++) {
134 
135  dv += exp(-p * (vec[i] - v_min)) * dvec[i];
136  v += exp(-p * (vec[i] - v_min));
137  }
138 
139  if (comm) MAST::Numerics::Utility::comm_sum(*comm, dv);
140  if (comm) MAST::Numerics::Utility::comm_sum(*comm, v);
141 
142  v = dv / v;
143 
144  return v;
145 }
MAST::Numerics::Utility::real_minimum
real_t real_minimum(const std::vector< real_t > &vec)
computes minimum of vector
Definition: utility.hpp:92
MAST::Numerics::Utility::comm_min
real_t comm_min(const libMesh::Parallel::Communicator &comm, const std::vector< real_t > &v)
Definition: utility.hpp:382
uint_t
unsigned int uint_t
Definition: mast_data_types.h:43
MAST::Numerics::Utility::comm_sum
void comm_sum(const libMesh::Parallel::Communicator &comm, real_t &v)
Definition: utility.hpp:328

◆ aggregate_minimum_sensitivity() [3/4]

template<typename ScalarType >
ScalarType MAST::Optimization::Aggregation::aggregate_minimum_sensitivity ( const std::vector< ScalarType > &  vec,
const uint_t  i,
const real_t  p,
const ScalarType &  denom,
const ScalarType &  v_min 
)

computes sensitivity of aggregated minimum of values specified in vector vec with respect to i th value.

The aggregation constant is p. The aggregation expression used is

\[ \frac{d v_{agg}}{d v_j} = \frac{ \exp (-p (v_j - v_{min})) }{ \sum_i \exp (-p (v_i - v_{min})) } \]

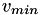, where, $ v_{min} $ is the minimum value out of all values in vec. This method differs from the other in that the user provides the cached denominator of the sensitivity and the minimum value in denom and v_min.

Definition at line 192 of file discrete_aggregation.hpp.

196  {
197 
198  return exp(-p * (vec[i] - v_min)) / denom;
199 }

◆ aggregate_minimum_sensitivity() [4/4]

template<typename ScalarType >
ScalarType MAST::Optimization::Aggregation::aggregate_minimum_sensitivity ( const libMesh::Parallel::Communicator *  comm,
const std::vector< ScalarType > &  vec,
const std::vector< ScalarType > &  dvec,
const real_t  p,
const ScalarType &  denom,
const ScalarType &  v_min 
)

computes sensitivity of aggregated minimum of values specified in vector vec with respect to parameter 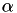$ \alpha $.

The aggregation constant is p. The sensitivity of values with respect to parameter is provided in dvec. The sensitivity expression used is

\[ \frac{d v_{agg}}{d p} = \frac{ \sum_j \exp (-p (v_j - v_{min})) \frac{dv_j}{d\alpha} }{ \sum_i \exp (-p (v_i - v_{min})) } \]

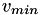, where, $ v_{min} $ is the minimum value out of all values in vec. This method differs from the other in that the user provides the cached denominator of the sensitivity and the minimum value in denom and v_min. If comm is a non-null pointer then the computation is synchronized across all ranks with the summation obtained from a collective.

Definition at line 217 of file discrete_aggregation.hpp.

222  {
223 
224  ScalarType
225  dv = 0.;
226 
227  for (uint_t i=0; i<vec.size(); i++) {
228 
229  dv += exp(-p * (vec[i] - v_min)) * dvec[i];
230  }
231 
232  if (comm) MAST::Numerics::Utility::comm_sum(*comm, dv);
233 
234  return dv / denom;
235 }
uint_t
unsigned int uint_t
Definition: mast_data_types.h:43
MAST::Numerics::Utility::comm_sum
void comm_sum(const libMesh::Parallel::Communicator &comm, real_t &v)
Definition: utility.hpp:328